Handwritten Digits Recognition using Machine Learning
Automated handwritten digit recognition is widely used today - from recognizing zip codes (postal codes) on mail envelopes to recognizing amounts written on bank checks. This project will show how a methods of Machine Learning such as one-vs-all logistic regression and neural networks are used to recognize hand-written digits.
The next diagram describe phases of a Recognition System:
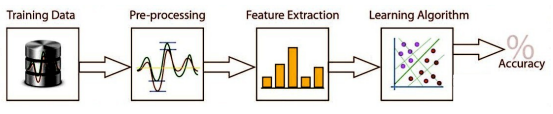
Figure 1: Recognition System
Training Data
This recognition system will use a data training that contains 5000 training examples of handwritten digits. Each training example is a 20 pixel by 20 pixel grayscale image of the digit. Each pixel is represented by a floating point number indicating the grayscale intensity at that location. The 20 by 20 grid of pixels is “unrolled” into a 400-dimensional vector. Each of these training examples becomes a single row in our data matrix *X*. This gives us a 5000 by 400 matrix *X* where every row is a training example for a handwritten digit image.
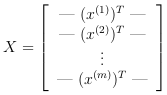
The second part of the training set is a 5000-dimensional vector *y* that contains labels for the training set. A “0” digit is labeled as “10”, while the digits “1” to “9” are labeled as “1” to “9” in their natural order.
To visualize a subset of the training set, the code randomly selects selects 100 rows from *X* and passes those rows to display the data. This maps each row to a 20 pixel by 20 pixel grayscale image and displays the images together. After this step, an image will be displayed like next figure:

Figure 2: Visual Training Data
Vectorizing Logistic Regression
This recognition system will use multiple one-vs-all logistic regression models to build a multi-class classifier. Since there are 10 classes, recognitio system will need to train 10 separate logistic regression classifiers. To make this training efficient, the code will be vectorized. To get a better performance, this recognition system implements a vectorized version of logistic regression that does not employ any "for" loops.
- Vectorizing the cost function: Recognition system is used a vectorized version of the cost function. Recall that in (unregularized) logistic regression, the cost function is:
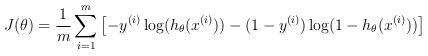
where:
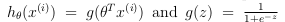
To compute each element in the summation, we have to compute last terms for every example 'i'. It turns out that this can be compute quickly for all our examples by using matrix multiplication. Defining 'X' and 'θ' as:
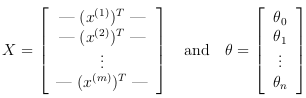
Then, by computing the matrix product Xθ:
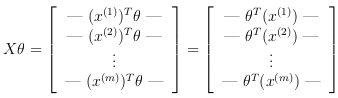
In the last equality, the fact that a^T.b = b^T.a is used, where a and b are vectors. This allows to compute the products θ^T.x(i) for all our examples 'i' in one line of code.
The last strategy is used to calculate θ^T.x(i) .
- Vectorizing the gradient: Recall that the gradient of the (unregularized) logistic regression cost is a vector where the 'jth' element is defined as:
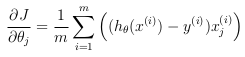
To vectorize this operation over the dataset, all the partial derivatives will be written explicitly for all 'θj':
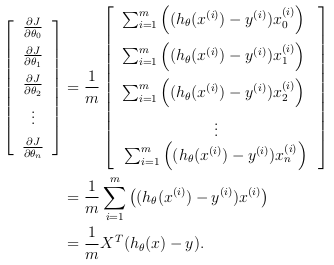
where:
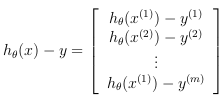
To understand the last step of the derivation:
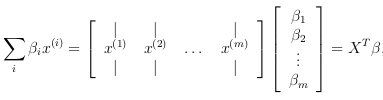
where:
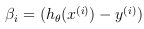
The expression above allows to compute all the partial derivatives without any loops.
- Vectorizing regularized logistic regression: It will be used to add regularization to the cost function. Recall that for regularized logistic regression, the cost function is defined as:
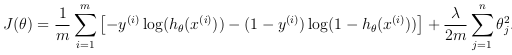
Note that θ0 is not regularized, which is used for the bias term.
Correspondingly, the partial derivative of regularized logistic regression cost for 'θj' is defined as:
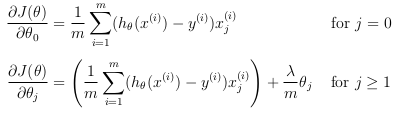
Last strategy helps to not employ any "for" loops.
One-vs-all Classification
One-vs-all classification is implemented by training multiple regularized logistic regression classifiers, one for each of the K classes in our dataset (Figure 2).
In this recognition system, one classifier is trined for each class. In particular, code returns all the classifier parameters in a matrix Θ of dimension K×(N+1), where each row of Θ corresponds to the learned logistic regression parameters for one class.
- One-vs-all Prediction: After training one-vs-all classifier, it is used to predict the digit contained in a given image. For each input, code computes the “probability” that it belongs to each class using the trained logistic regression classifiers. One-vs-all prediction function picks the class for which the corresponding logistic regression classifier outputs the highest probability and return the class label (1, 2,..., or K) as the prediction for the input example. With the learned value of Θ the recognition systemgets the training set accuracy of 94.9%:
Training Set Accuracy: 94.990000
Program paused. Press enter to continue.
Neural Networks
In the previous part, recognition system was implemented with a multi-class logistic regression to recognize handwritten digits. However, logistic regression cannot form more complex hypotheses as it is only a linear classifier.
In this part, a neural network is implemented to recognize handwritten digits using the same training set as before. The neural network will be able to represent complex models that form non-linear hypotheses. This project uses parameters from a neural network that we have already trained. The focus is the implementation of the feedforward propagation algorithm to use weights for prediction.
The neural network used in this recognition system is shown in Figure 3. It has 3 layers – an input layer, a hidden layer and an output layer. Recall that inputs are pixel values of digit images. Since the images are of size 20×20, this gives us 400 input layer units (excluding the extra bias unit which always outputs +1). As before, the training data is loaded into the variables 'X' and 'y'.
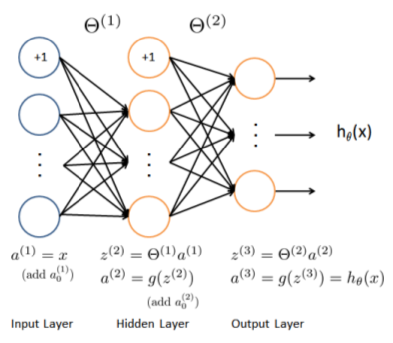
Figure 3: Neural Network Model
This recognition system has an accuracy of 97.5%. The next result from Octave shows this:
Training Set Accuracy: 97.520000
Program paused. Press enter to continue.
When run the code in Octave, an interactive sequence is launched displaying images from the training set one at a time, while the console prints out the predicted label for the displayed image:
Test for the number 2:

Test for the number 5:

Test for the number 7:
